Trigonometrice Formula - lista cu formule de bază

Raporturile dintre funcțiile trigonometrice de bază - sinus, cosinus, tangenta, cotangentă, și - set formule trigonometrice. Și, din moment ce relațiile dintre funcțiile trigonometrice o mulțime, atunci acest lucru explică abundența de formule trigonometrice. Unele formule trigonometrice funcțiile de conectare la același unghi, celălalt - funcția multiplă a unghiului, și altele - face posibilă scăderea gradului, al patrulea - să-și exprime toate funcțiile prin tangenta jumătate de unghi, etc.

In acest articol vom enumera în ordinea tuturor principalelor formule trigonometrice, care sunt suficiente pentru a aborda marea majoritate a problemelor trigonometrie. Pentru ușurința de depozitare și de utilizare trebuie să fie grupate în funcție de destinația prevăzută, și le-a pus în tabel.

Navigare în pagină.

identitățile trigonometrice de bază

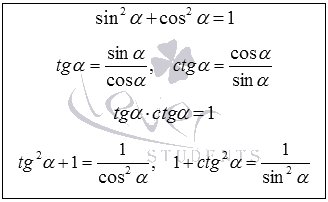
identitățile trigonometrice de bază stabilite relații între sinus, cosinus, tangenta și cotangentă unghiului. Ele sunt derivate din definiția sinus, cosinus, tangentă și cotangentă și concepte ale cercului unitate. Acestea permit o să-și exprime funcția trigonometrică prin orice alta.

Descrierea detaliată a formulelor de trigonometrie și exemplele lor de derivare și de aplicare, a se vedea articolul identitățile trigonometrice de bază.

formulele de reducere

Formulele de reducere rezultă din proprietățile sinus, cosinus, tangentă și cotangentă. adică, ele reflectă proprietatea periodicității funcțiilor trigonometrice, simetria proprietății, precum și proprietatea de offset la un anumit unghi. Aceste formule trigonometrice permit să lucreze cu unghiuri arbitrare muta pentru a lucra cu unghiuri în intervalul de la zero la 90 de grade.

Fundamentare aceste formule mnemonic pentru stocarea și exemple de aplicare a acestora acestora pot fi explorate in articol aduce formula.

formule de adiție

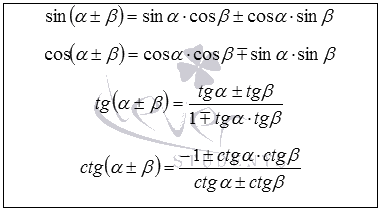
formule de adiție trigonometrice arată sumă funcții cum trigonometrice sau diferența dintre cele două unghiuri exprimate în ceea ce privește funcțiile trigonometrice de unghiuri. Aceste ecuații servesc drept bază pentru a obține următoarele formule trigonometrice de mai jos.

Pentru mai multe informații în articolul adăugând formule.

Formula de duble, triple, etc. unghi

Formula de duble, triple, etc. Unghiul (numite și mai multe formule de unghi) arată modul în care funcțiile trigonometrice de binare, ternare, etc. Unghiul () sunt exprimate în termeni de funcții trigonometrice singur unghi. Concluzia lor se bazează pe formulele de adiție.

formula Half-unghi

Jumătate unghi formula arată modul în care funcțiile trigonometrice sunt exprimate prin jumătatea unghiului unui cosinusul unghiului. Aceste formule trigonometrice rezultă din unghiul dublu.

derivare și aplicarea lor exemple pot fi găsite în articolul din Formula jumătate de unghi.

Coborârea formula

formule trigonometrice menite să reducă gradul de a facilita tranziția de la puterile naturale ale funcțiilor trigonometrice la sinus și cosinus în primul grad, dar unghiuri multiple. Cu alte cuvinte, ele permit grad mai scăzut la primele funcții trigonometrice.

Formula sumă și diferență de trigonometrice

Scopul principal al sumei și diferența de formule ale funcțiilor trigonometrice este de a comuta la caracteristicile produsului, care sunt foarte utile în simplificarea expresiilor trigonometrice. Aceste formule sunt, de asemenea, utilizate pe scară largă în rezolvarea ecuațiilor trigonometrice, deoarece acestea permit să se stabilească suma factorizarea și diferența dintre sinus și cosinus.

Derivarea formule și exemple de aplicare a acestora, a se vedea articolul din Formula sumă și diferență sinus și cosinus.

Formula produs de sine, cosinus și sinus și cosinus

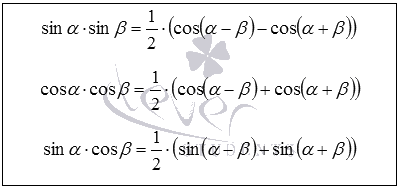
Tranziția de la produsul funcțiilor trigonometrice la suma sau diferența realizată de Formulele lucrări sinus, cosinus și cosinus sine.

substituție universal trigonometrice

Prezentare generală a principalelor formule trigonometrice se încheie cu revendicările care exprimă funcții trigonometrice în ceea ce privește tangenta unghiului jumătate. Această înlocuire se numește substituție trigonometrice universală. confortul său este faptul că toate funcțiile trigonometrice exprimate prin tangenta unghiului jumătate rațional, fără rădăcini.