Soluția de ecuații în numere întregi - matematică

Proiectul meu curs este dedicat uneia dintre cele mai interesante secțiuni ale teoriei numerelor - soluția de ecuații în numere întregi.

Soluție în numere întregi de ecuații algebrice cu coeficienți întregi, cu mai mult de un necunoscut este una dintre cele mai dificile probleme din teoria numerelor.

Problema de a rezolva ecuații în numere întregi complet rezolvate numai pentru ecuațiile de gradul al doilea în două necunoscute. Rețineți că, pentru ecuațiile de orice grad cu o singură necunoscută nu reprezintă nici un interes substanțial, deoarece această problemă poate fi rezolvată prin utilizarea unui număr finit de eșantioane. Pentru ecuațiile de mai sus de gradul al doilea, cu două sau mai multe necunoscute este foarte dificil, nu numai la problema găsirii tuturor soluții în numere întregi, dar chiar și o sarcină simplă de a stabili existența unui set finit sau infinit a unor astfel de soluții.

În proiectul meu am încercat să subliniem câteva dintre principalele rezultate obținute în teoria; rezolvarea ecuațiilor în numere întregi. Teorema formulate în ea, sunt prevăzute cu probe în cazurile în care probele destul de simplu.

1. ecuație cu o singură necunoscută

Luați în considerare ecuația de gradul I cu o singură necunoscută

Lăsați coeficienții ecuației și - numere întregi. In mod clar, soluția acestei ecuații

Acesta este un număr întreg numai dacă este divizibil cu. Astfel, ecuația (1) nu este întotdeauna solubilă în numere întregi; de exemplu, de două ecuații și prima soluție are un întreg și un al doilea număr întreg insolubil.

Cu aceeași împrejurare ne întâlnim în cazul ecuațiilor de grad mai mare decât prima: ecuația pătratică are soluții întregi; ecuație în numere întregi este unsolvable, deoarece rădăcinile sale sunt iraționale.

Problema găsirii rădăcinile ecuației la fel de mult ca și gradul n-lea cu coeficienți întregi

Este ușor de rezolvat. Într-adevăr, chiar și - o rădăcină a acestei ecuații. atunci

Din ultima ecuație arată că divizibil; De aceea, fiecare rădăcină a ecuației (2) este o ecuație termen constant compas. Pentru a găsi soluțiile întregi ale ecuației este necesar să se selecteze acele subgrupuri care, atunci când substituit în ecuația devine o identitate. De exemplu, numerele 1, -1, 2, -2, reprezentând toate divizorii ecuația termen constant

Numai -1 este o rădăcină. Prin urmare, această ecuație are o singură rădăcină. Aceeași metodă este ușor de a arăta că ecuația

în numere întregi este de nerezolvat.

De mult interes mai mare este decizia în numere întregi ale ecuației cu multe necunoscute.

Citește mai mult: ecuația de gradul întâi cu două necunoscute

Informații despre „soluția de ecuații în numere întregi“

Categorie: Matematică
Numărul de caractere, inclusiv spații: 24303
Număr de mese: 27
Numărul de imagini: 7

sub formă de rețete, nici un indiciu cu privire la modul în care au fost găsite. In ciuda nivelului ridicat de dezvoltare a algebrei în Babilon, în textele cuneiforme • nu există nici un concept al unui număr negativ, precum și metode generale de rezolvare a ecuațiilor de gradul doi. Așa cum sa decis Diophant și ecuații pătratice. Accesând „Aritmetica“ Diophant expoziția nu sistematică de algebră, dar conține.

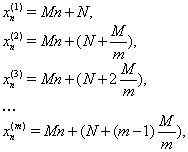
conversie revizuite grupurile fractionare soluții comune ecuații trigonometrice. A treia secțiune se referă la ecuații trigonometrice non-standard, care se bazează pe soluțiile de abordare funcționale. A patra secțiune se referă la inegalitatea trigonometrice. Detalii discutat metode soluții trigonometrice elementare ale inegalităților, ca o unitate de cerc, și așa mai departe.

;. și anume ; O soluție generală. în cazul în care. Metoda 2: Luați în considerare un alt mod de a găsi soluții LDE cu două necunoscute, iar pentru aceasta considerăm ecuația de forma. Ecuațiile de acest tip sunt numite liniare ecuații Diofantine omogene (liniare Ecuatii diferentiale ordinare). Exprimându-necunoscut. prin a ajunge la necunoscut Deoarece x trebuie să fie un număr întreg, unde -. un întreg arbitrar. Mijloace.

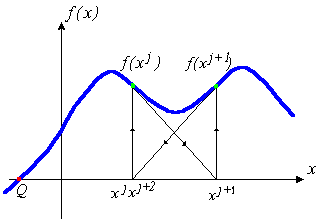
în cazul în care punctul de abordare inițială este departe de punctul de soluție, metoda lui Newton - Raphson nu poate converge deloc. Interpretarea geometrică nu este convergent Newton - metoda Raphson este prezentată în Fig. 1b. Assignment Algoritm: găsirea unei soluții a ecuației (1) Intrare: inițială Precizia de aproximare x0 (număr de iterații I) Output: xI - soluția ecuației (1) Inițializarea: calcula f „(x0) Pași.