Lecția - soluția de ecuații liniare cu două variabile în numere întregi

O scurtă descriere a documentului:

Este cunoscut faptul că marea majoritate a acestor ecuații sunt setul de răspunsuri furnizate întotdeauna o pereche de numere. Cuplul - valorile lui x și y. opțiuni pentru rădăcinile următoarele Luați în considerare:

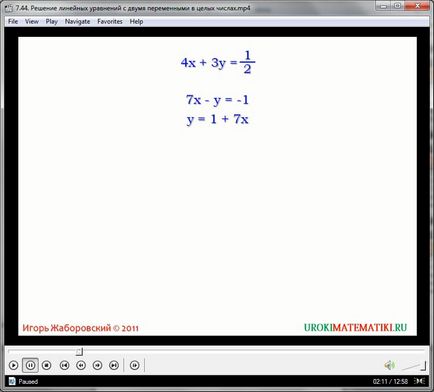
Evident, rădăcinile ecuației poate fi o pereche (4, 6):

Sau fracțiuni de 1/5 și 1/3:

5 (1/5) - 3 (1/3) = 2

În ambele cazuri, o adevărată egalitate, atunci ambele perechi de rădăcini sunt soluții acceptabile așa cum este reprezentat de ecuația. Dar aceasta este o pereche de fracțiuni, iar al doilea reprezentat de numere întregi. Rădăcinile ecuații cu două variabile, cu valori în numere întregi numite integral numerice.
Destul de des, în matematică sunt sarcini care necesită exact soluțiile întregi ale unor astfel de ecuații. Pe de altă parte, unele variații cum ar fi:

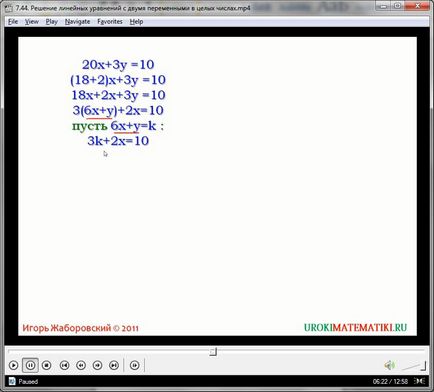
Nu au o bucată de soluții numerice, în general. Deoarece pentru orice întreg x și y se va transforma toată partea stângă a expresiei generale (2x + 3y), care nu poate fi egală cu o fracțiune - adică încălcarea principiului păstrării egalității.
Să considerăm posibilă soluție a ecuației:

Traduceți aceasta într-o formă în funcție de transportul prin semnul de egalitate și identitate transformări:

Este evident că există în continuare un fel de egalitate:

În cazul în care n - orice număr întreg, care poate fi bine un număr întreg de valoare. Aceasta este, 7x ecuație - y = -1 are multe soluții întregi. Verificăm orice numere întregi x ca:

Știm deja formula abstractă generală pentru determinarea oricăror ecuații liniare cu două variabile:

Acolo unde x și y - variabile și b - coeficienții variabilelor, și - pe termen liber. Orice ecuație expresie liniară similară cu x și y prin modificări echivalente pot duce la o asemenea formă abstractă. Un studiu detaliat al formulei îl face ușor de a identifica anumite modele în ceea ce privește disponibilitatea soluțiilor întregi. Deci, dacă ni se dă o anumită ecuație de forma:

În care termenul liber este o fracție, rădăcinile ecuației nu poate fi niciodată expresie numerică întreagă. Suma sau diferența dintre două numere întregi prin lege algebra elementară nu poate fi egal cu expresia fracționată.

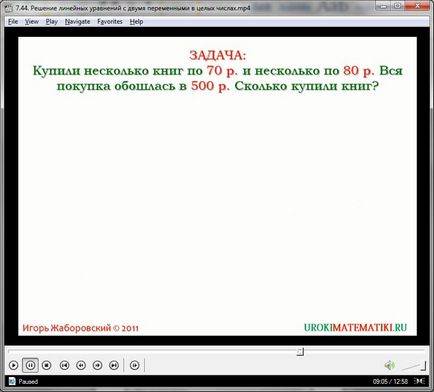
Din cauza numărului mare de soluții posibile, rădăcinile ecuații cu două variabile nu sunt, uneori, formează perechi separate de numere și o pereche de două formule individuale - pentru x și y. De exemplu, să rezolve ecuația:

Pentru a face acest lucru, avem nevoie pentru a face o serie de modificări. Împărțim monom 20x la 18x sumă identică + 2:

18x + 2x + 3y = 10

Grupul de monoamele având multiple coeficienți numerici. Trebuie remarcat faptul că variabila x trebuie defalcate în suma astfel încât x să fie transformat cu un factor cât mai mare posibil și, astfel, să se plieze coeficientul numeric al variabilei y. Deoarece în exemplul nostru ar trebui să aibă trei, atunci x vom rupe cu multiplul maxim admisibil coeficientul de trei. După ce grupul ia un factori multipli comuni:

18x + 2x + 3y = 10

18x + 3y + 2 = 10

Lăsați expresia în paranteze (6x + y) este egală cu o anumită variabilă, atunci:

Se împarte valoarea variabilei cu același principiu ca și coeficientul lui x rupte. În același timp, avem nevoie pentru a ridica un anumit număr care este un multiplu de două (valoare la 2), dar nu mai mult de trei. Evident, ar fi aceasta:

Organizăm modificări identice:

Parantezele reprezintă conținutul, ca n, ora:

Substitut egalitatea rezultată în loc cu:

3 (10 - 2n) + 2 = 10

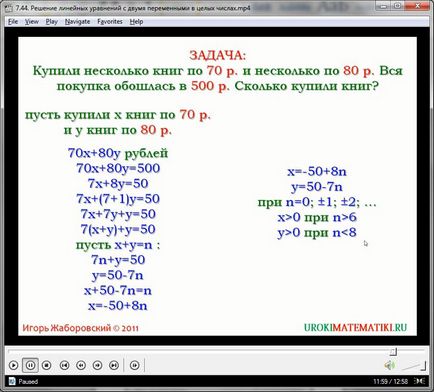
Și de a rezolva ecuația rezultată pentru variabila x:

3 (10 - 2n) + 2 = 10

30 - 6n + 2 = 10

2 = 10 + 6n - 30

Este necesar să se înregistreze:

6x + y = n - x

Substitut cunoscut nouă formula pentru x, care va fi calculată din:

6x + y = n - x

6 (- 10 + 3n) + y = n - (- 10 + 3n)

-60 + 18N + y = n + 10 - 3n

y = n + 10 - 3n + 60 - 18N

Rădăcinile ecuației 20x + 3y = 10 sunt două expresii ale formei:

În cazul în care n - orice număr întreg - 0, 1, 2, etc. Astfel, pentru a descrie diversitatea soluțiilor posibile întregi, cel mai simplu mod de a calcula o formulă de calcul rapid al lui x și y. Substituind orice expresie n în aceste formule se pot obține cu ușurință perechea dorită de numere.