funcţii trigonometrice
Funcții trigonometrice într-un triunghi dreptunghic
Pentru a determina funcțiile trigonometrice de un unghi arbitrar α, luați un triunghi arbitrar în unghi având un unghi α. această latură a triunghiului va fi numit după cum urmează:
Ipotenuză - partea opusă unghiului drept, cea mai lungă latură a triunghiului. În acest caz, partea c.
Partea opuse - picior, care se află vizavi de colț. De exemplu, piciorul unui - în raport cu colțul opus al A.
lateral adiacent - piciorul, care este un unghi lateral. De exemplu, piciorul b - adiacent unghiului A.
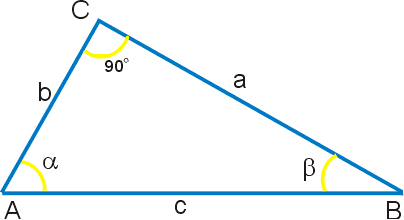
Presupunem că triunghiul este în planul euclidian, astfel încât suma unghiurilor este egală cu π. Aceasta înseamnă că unghiurile dintre picioare și ipotenuza sunt între 0 și π / 2. Folosind definiția formulei sau de conducere prin cercul unitate, se poate extinde domeniul funcțiilor trigonometrice în setul de numere reale.
Sinusul unghiului - relația piciorului opus ipotenuzei: Acest raport este independent al triunghiului ABC cuprinzând un unghi α, deoarece toate aceste triunghiuri sunt similare.
Cosinusul unghiului - raportul dintre ipotenuzei a piciorului adiacent: Deoarece sinusul unghiului ascuțit al triunghiului este egal cu cosinusul al doilea, și vice-versa.
Tangenta unghiului - raportul dintre piciorul opus unui adiacent:
Unghiul cotangentă - relația piciorului adiacent unui opus: cotangentă un unghi ascuțit într-un triunghi dreptunghic este egal cu tangenta al doilea, și vice-versa.
Unghiul secantă - raportul dintre ipotenuzei cu piciorul adiacent:
Unghiul cosecant - raportul dintre ipotenuzei la piciorul opus:
Definirea funcțiilor trigonometrice prin cercul
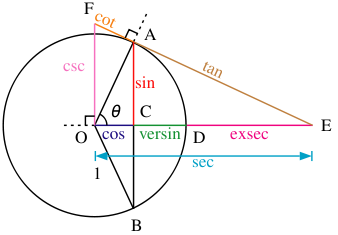
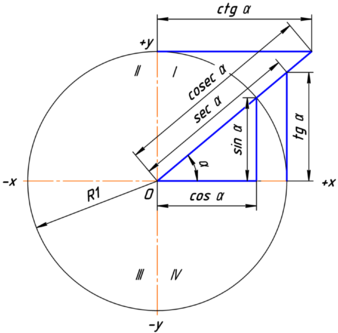
Unghiul secantă este raportul dintre lungimea segmentul OA la abscisei punctului A. Deoarece Se indică lungimea segmentului OA este 1, secantă egal cu inversul cosinusul:
Din definiția rezultă că, dacă cosinusul unghiului este zero, tangenta și secant acestui unghi nu există. În mod similar, pentru cotangentă și cosecant dacă sinusul unghiului este zero, cotangentă și cosecant acest unghi nu există.
Să presupunem că planul dreptunghiular sistem de coordonate definit cu originea în punctul O și axele OX și OY. Luați în acest sistem de coordonate cerc cu centrul la O și o rază egală cu unu. Să segmentul OA este rotit la orice unghi în jurul centrului O.
Sinusul unghiului este raportul dintre ordonata punctului A la lungimea segmentului OA. Deoarece lungimea a denota segmentul OA este 1,
Cosinusul unghiului este raportul dintre punctul abscisa A la lungimea segmentului OA. Deoarece lungimea a denota segmentul OA este 1,
Tangenta unghiului este raportul dintre punctul ordonatei abscisă A la punctul A. Desemnat (în literatura engleză, deoarece atât
Unghiul cotangentă este raportul dintre punctul abscisa A la punctul A. ordonata este (în literatura engleză, deoarece atât cotangentă este inversul tangentei:
Unghiul cosecant este raportul dintre lungimea segmentului OA de ordonata A. este (în literatura engleză Deoarece lungimea segmentul OA este 1, cosecant egal cu inversul sinusul:
Definirea funcțiilor trigonometrice prin rândurile
Folosind geometria și proprietățile limitelor poate demonstra că derivata cosinus și sinus este egală cu derivata cosinusul este sinus negativ. Apoi putem folosi teoria seriilor Taylor și la sinusul și cosinusul suma seriei de puteri:
Folosind aceste formule și ecuații și pot găsi de expansiune de serie Taylor și alte funcții trigonometrice:
în cazul în care Bn - numerele Bernoulli.
în cazul în care En - numerele Euler.
Valorile funcțiilor trigonometrice pentru anumite unghiuri