formule trigonometrice
Interrelaționării funcțiilor trigonometrice de bază, care atât cosinus și sinus, tangenta și cotangentă - numite formule trigonometrice. Datorită faptului că un număr foarte mare de interrelații, respectiv, iar formula nu este mai mic. formule piesa combină funcțiile trigonometrice în funcție de unghiul, care poate fi fie un multiplu sau la fel. Acesta poate fi, de asemenea, exprimată prin tangenta unghiului jumătate. Doar prin reducerea gradului.
Vom analiza cele mai multe formule trigonometrice de bază. Cu ajutorul cărora puteți rezolva cele mai multe dintre sarcinile trigonometrice. Pentru mai mult confort, le combina cu valoare, conform tabelelor.
Să începem cu identități trigonometrice.
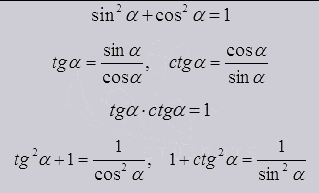
Bazele în identități trigonometrice sinus determinată relație și cosinus, tangentă și cotangentă într-un colț. Și din definiția lor și cercul unitate. Oferă o oportunitate de a evidenția prin orice altă funcție.
Apoi, ia în considerare trigonometrice formule acționare.
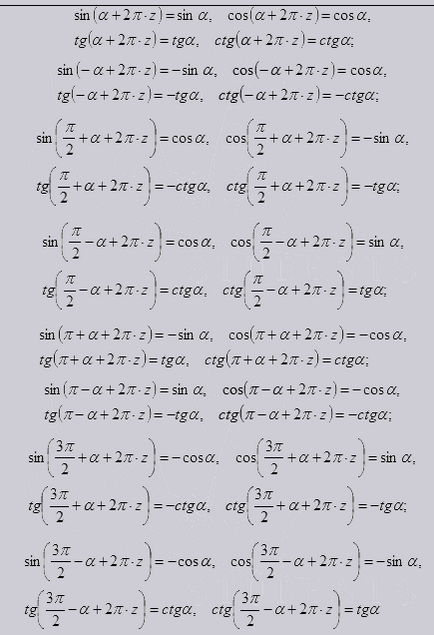
Ele derivă din proprietățile sinus, cosinus, și tangentele cotangents. aceasta exprimându-și proprietăți astfel de funcții ca: frecvență, simetrie și trecerea la dreapta în cauză. oferă, de asemenea, o oportunitate de a lucra cu unghiuri în intervalul de până la 90 de grade și unghiuri arbitrare.
Formula pentru completare.
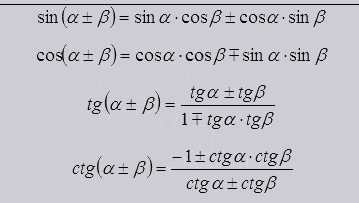
Din aceste formule este evident că funcțiile suma sau diferența dintre cele două unghiuri sunt derivate din ele ca funcții trigonometrice. Este, de asemenea, baza pentru formulele binare, ternare și alte unghiuri.
Formula pentru binar, ternar și alte unghiuri.
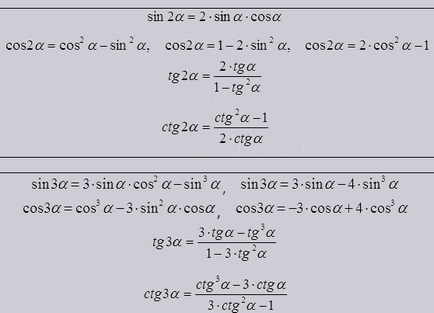
Ele arată că funcția trigonometrică a unghiului dublu, triplu, sau orice fel de derivat din TF unghiuri unice.
La fel ca single, duble, triple, etc. acolo și unghiuri jumătate
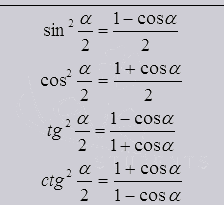
Din formulele de jumătate de unghi, vedem că el iese din cosinusul unghiului întregului.
La fel cum există grade de metode de reducere a arata ca:
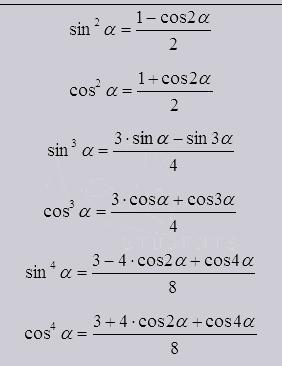

Cu utilizarea lor poate reduce funcția de gradul întâi. Interactiunea cu puterea naturală a funcției de a traduce doar sinus și cosinus din mai multe unghiuri, în primul grad.
Suma și diferența unei funcții trigonometrice.
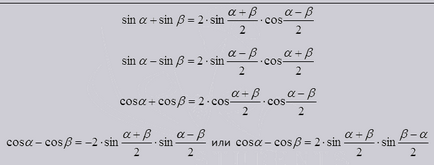
Ajuta la simplificarea expresiei trigonometrice, și la factorul sinus și cosinus.
Produsul de sine, cosinus, și unul pentru celălalt.
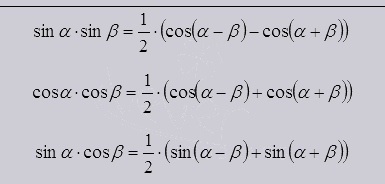
Metoda de substituție trigonometrice universale.
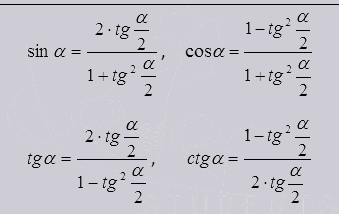
O astfel de substituție este convenabilă deoarece funcțiile sunt obținute fără rădăcini.