Discretă variabile aleatoare
variabilă aleatoare numită valoare variabilă, care este un rezultat al fiecărui test în avans, are o valoare necunoscută, care depinde de cauze accidentale. Variabile aleatoare sunt notate cu litere latine majuscule: $ X, \ Y, \ Z, \ \ puncte $ În funcție de tipul lor de variabile aleatoare poate fi discret și continuu.
variabilă aleatoare discretă - este o variabilă aleatoare a cărei valori pot fi nu mai mult numărabil, care este fie finit sau numărabil. Sub numărabilitate ceea ce înseamnă că valorile variabilei aleatoare pot fi enumerate.
Exemplul 1. Iată câteva exemple de variabile aleatoare discrete:
a) numărul de hit-uri țintă la $ n $ fotografii sunt valorile posibile ale $ 0, \ 1, \ \ puncte, \ n $.
b) numărul de straturi de arme la tragerea la sorti căzută, unde valorile posibile ale $ 0, \ 1, \ \ puncte, \ n $.
c) numărul de sosiri la bordul navelor (set numărabilă de valori).
g) numărul de apeluri care vin la centrala telefonică (set numărabilă de valori).
1. Legea distribuției de probabilitate discretă a variabilei aleatoare.
Un discret aleatoare variabila $ X $ poate lua valorile $ x_1, \ puncte, \ x_n $ cu probabilitate $ p \ stânga (x_1 \ dreapta), \ \ puncte, \ p \ stânga (x_n \ dreapta) $. Corespondența între aceste valori și probabilitățile lor se numește legea unei variabile aleatoare discrete. De regulă, această corespondență este dată de tabelul din primul rând de care indică valorile $ x_1, \ puncte, \ x_n $, iar a doua linie corespunzătoare acestor valori de probabilitate $ p_1, \ puncte, \ p_n $.
$ \ Începe
\ hline
X_i x_1 x_2 \ puncte x_n \\
\ hline
p_i p_1 p_2 \ puncte p_n \\
\ hline
\ End $
Exemplul 2. Să variabila aleatoare $ X $ - numărul de puncte a scăzut la aruncarea unui zar. O astfel de variabilă aleatoare X $ $ poate lua următoarele valori $ 1 \ 2 \ 3 \ 4 \ 5 \ 6 $. Probabilitatea ca toate aceste valori sunt egale cu 1 $ / 6. Apoi, legea de distribuție a aleatoare $ variabila X $:
$ \ Începe
\ hline
1 2 3 4 5 6 \\
\ hline
1/6 1/6 1/6 1/6 1/6 1/6 \\
\ hline
\ End $
2. Așteptarea unei variabile aleatoare discrete.
Așteptarea cantității aleatoare definește valoarea sa „centru“. Pentru o așteptare variabilă aleatoare discretă se calculează ca suma valorilor $ x_1, \ dots, \ x_n $ corespunzătoare acestor valori de probabilitate $ p_1, \ puncte, \ p_n $, adică: $ M \ stânga (X \ dreapta) = \ sum ^ n_ $. În literatura de specialitate în limba engleză, folosind o altă notație $ E \ stânga (X \ dreapta) $.Proprietățile speranța de $ M \ stânga (X \ dreapta) $:
- $ M \ stânga (X \ dreapta) $ se află între cele mai mici și cele mai mari valori ale variabilei aleatoare X $ $.
- Așteptarea cea mai constantă este constantă, adică, $ M \ stânga (C \ dreapta) = C $.
- Un factor constant poate fi luat ca un semn de așteptare matematice: $ M \ stânga (CX \ dreapta) = CM \ stânga (X \ dreapta) $.
- Așteptarea matematică a sumei variabilelor aleatoare este egală cu suma așteptărilor lor matematice: $ M \ stânga (X + Y \ dreapta) = M \ stânga (X \ dreapta) + M \ stânga (Y \ dreapta) $.
- Așteptarea matematică a produsului de variabile aleatoare independente este egală cu produsul dintre așteptările lor matematice: $ M \ stânga (XY \ dreapta) = M \ stânga (X \ dreapta) M \ stânga (Y \ dreapta) $.
Exemplul 3. Ne găsim speranța unui $ variabila aleatoare X $ Exemplul $ 2 $.
Putem observa că $ M \ stânga (X \ dreapta) $ se află între cel mai mic ($ 1 $) și cea mai mare ($ $ 6) valori ale variabilei aleatoare X $ $.
Exemplul 4. Este cunoscut faptul că speranța matematică a unei variabile aleatoare este egală cu $ X $ $ M \ stânga (X \ dreapta) = $ sau 2. Găsiți speranța unei $ variabila aleatoare 3X + 5 $.
Folosind proprietățile de mai sus, pentru a primi $ M \ stânga (3X + 5 \ dreapta) = M \ stânga (3X \ dreapta) + M \ stânga (5 \ dreapta) = 3M \ stânga (X \ dreapta) + 5 = 3 \ cdot 2 + 5 = 11 $.
Exemplul 5. Este cunoscut faptul că speranța matematică a unei variabile aleatoare este egală cu $ X $ $ M \ stânga (X \ dreapta) = 4 $. Găsiți așteptarea unei variabile aleatoare $ 2X-9 $.
Folosind proprietățile de mai sus, pentru a primi $ M \ stânga (2X-9 \ dreapta) = M \ stânga (2X \ dreapta) -M \ stânga (9 \ dreapta) = 2M \ stânga (X \ dreapta) -9 = 2 \ cdot 4 -9 = -1 $.
3. Dispersia variabilei aleatoare discrete.
Valorile posibile sunt variabile aleatoare egal cu media pot varia împrăștiate în jurul valorilor lor medii. De exemplu, în două grupuri de studenți, scorul mediu pentru examen pe teoria probabilității a fost egal cu 4, dar într-un grup au fost toate horoshist, iar în celălalt grup - numai troechniki și onoruri. Prin urmare, este nevoie de astfel de caracteristici numerice ale variabilelor aleatoare, ceea ce ar demonstra răspândirea valorilor unei variabile aleatoare despre așteptările sale. O astfel de caracteristică este varianță.
Variația unei discrete variabila aleatoare $ X $ este:
În literatura de specialitate în limba engleză folosind notația $ V \ stânga (X \ dreapta), \ Var \ din stânga (X \ dreapta) $. Foarte des, dispersia $ D \ stânga (X \ dreapta) $ calculat cu formula $ D \ stânga (X \ dreapta) = \ sum ^ n ^ _- 2 $.proprietăți de dispersie a $ D \ stânga (X \ dreapta) $:
- Variația este întotdeauna mai mare sau egală cu zero, adică, $ D \ din stânga (X \ dreapta) \ ge 0 $.
- Dispersia constante este zero, adică $ D \ stânga (C \ dreapta) = 0 $.
- factor permanent poate fi luat ca un semn de dispersie cu condiția pătrat ea, adică $ D \ stânga (CX \ dreapta) = C ^ 2D \ stânga (X \ dreapta) $.
- Variația sumei de variabile aleatoare independente este egală cu suma varianțelor lor, adică, $ D \ din stânga (X + Y \ dreapta) = D \ stânga (X \ dreapta) + D \ stânga (Y \ dreapta) $.
- Variația diferenței de variabile aleatoare independente este egală cu suma varianțelor lor, adică, $ D \ stânga (X-Y \ dreapta) = D \ stânga (X \ dreapta) + D \ stânga (Y \ dreapta) $.
Exemplul 6. Calculăm variația variabila aleatoare X $ $ $ de la Exemplul 2 $.
Exemplul 7. Este cunoscut faptul că variația unei variabile aleatoare este egală cu $ X $ $ D \ din stânga (X \ dreapta) = $ sau 2. Găsiți variația variabilei aleatoare $ 4X + 1 $.
Folosind proprietățile de mai sus, găsiți $ D \ left (4X + 1 \ dreapta) = D \ stânga (4X \ dreapta) + D \ stânga (1 \ dreapta) = 4 ^ 2D \ stânga (X \ dreapta) + 0 = 16D \ stânga (X \ dreapta) = 16 \ cdot 2 = $. 32
Exemplul 8. Este cunoscut faptul că variația unei variabile aleatoare este egală cu $ X $ $ D \ din stânga (X \ dreapta) = 3 $. Găsiți varianța variabila aleatoare $ 3-2X $.
Folosind proprietățile de mai sus, găsiți $ D \ left (3-2X \ dreapta) = D \ stânga (3 \ dreapta) + D \ stânga (2X \ dreapta) = 0 + 2 ^ 2D \ stânga (X \ dreapta) = 4D \ stânga (X \ dreapta) = 4 \ cdot 3 = 12 $.
4. Funcția de distribuție a unei variabile aleatoare discrete.
Reprezentarea Metoda a distribuției variabile aleatoare discrete ca o serie nu este singurul, și cel mai important nu este universal, deoarece valoarea aleatoare continuă nu poate fi setată folosind o distribuție număr. Există un alt mod de reprezentare a variabilei aleatoare - Funcția de distribuție.
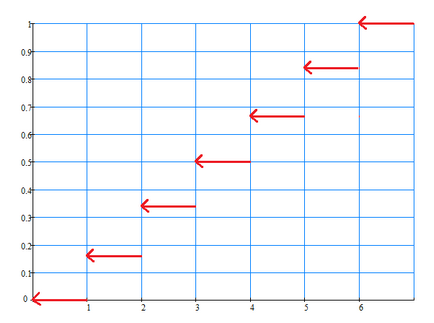
Funcția de distribuție a variabila aleatoare $ X $ este o funcție $ F \ stânga (x \ dreapta) $, care determină probabilitatea ca o variabilă aleatoare $ X $ ia o valoare mai mică decât o valoare fixă de $ x $, adică $ F \ stânga (x \ dreapta) = P \ stânga (X Proprietățile funcției de distribuție: Exemplul 9. Să ne găsim funcția de distribuție $ F \ stânga (x \ dreapta) $ pentru legea de distribuție a unei variabile aleatoare discrete $ X $ Exemplul $ 2 $. $ \ Începe Dacă $ x \ le 1 $, atunci, în mod evident, $ F \ stânga (x \ dreapta) = 0 $ (inclusiv la $ x = $ 1 $ F \ stânga (1 \ dreapta) = P \ stânga (X <1\right)=0$). Dacă $ de 1 Dacă $ cu 2 Dacă $ cu 3 Dacă $ cu 4 Dacă 5 $ Dacă $ x> 6 $, atunci $ F \ stânga (x \ dreapta) = P \ stânga (X = 1 \ dreapta) + P \ stânga (X = 2 \ dreapta) + P \ stânga (X = 3 \ dreapta) + P \ stânga (X = 4 \ dreapta) + P \ stânga (X = 5 \ dreapta) + P \ stânga (X = 6 \ dreapta) = 1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1/6 = 1 $. distribuție Program funcție $ F \ stânga (x \ dreapta) $:
\ hline
1 2 3 4 5 6 \\
\ hline
1/6 1/6 1/6 1/6 1/6 1/6 \\
\ hline
\ End $