Aria unui triunghi isoscel formula

În acest articol ne vom concentra pe modul de a găsi aria unui triunghi isoscel, iar formula pentru soluția.
triunghi isoscel este un triunghi care are două laturi paralele ale bazei sunt egale. El este reprezentat în figură.

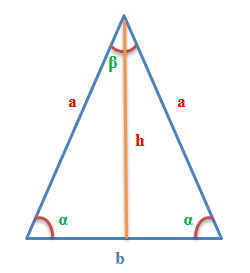
Trebuie remarcat faptul că scrisorile care au marcat laturile și unghiurile sunt utilizate în formule, pentru confortul dumneavoastră.

Suprafața unei formule triunghi isoscel.

Prima formulă spune că zona este, dacă suntem conștienți de doar o parte și baza triunghiului. Am primit această formulă prin utilizarea formulei. În cazul în care primar este formula Heron și partea laterală a figurii sunt egale, ea se va arăta mai ușor.

În a doua formulă pentru a menționa faptul că zona este peste părțile laterale și fiind unghiul dintre ele. Sau unghiul de păcat situat între părți, înmulțită cu jumătate din piața uneia dintre părți. Atunci când înălțimea firului de pe partea laterală a lungimii sale este un păcat *. Având în vedere că lungimea laturii, știm că și știm înălțimea sa. Prin urmare, aria unui triunghi isoscel este jumătate din expresia lor. Pentru a fi mai precis. întreaga valoare a face zona de triunghi. Partajarea înălțimea dreptunghiului, obținem două triunghiuri drepte nu sunt mari. partea diagonală a triunghiului va fi la rândul său, îl împarte cifra în două părți egale. Din care rezultă că valoarea solicitată este de mărime ca jumătate de o parte, înmulțită cu înălțimea.

A treia formulă este zona paralelă cu o singură mână, iar unghiul de bază fiind pe partea de sus. Cu alte cuvinte, putem spune acest lucru: atunci când cunoaște cel puțin un unghi de triunghi isoscel, cu ajutorul acestuia puteți cunoaște celelalte două. Această formulă este similară cu cea de a doua formulă, ar putea fi folosite pentru a aminti oricare dintre ele. Dar această formulă vin a cincea, pe care o voi descrie mai jos.

Formula a patra arată că zona poate fi găsită cunoscând valoarea unei baze și într-un unghi în acesta. Toate colțurile din partea inferioară aceeași parte a bazei și pătrat este împărțit în unghi etaj 4 tg, care a apărut pe laturile sale. Când cu atenție pentru a vedea, puteți vedea partea de bază podea b / 2, când tg multiplicată (? / 2) dă înălțime. Care, la rândul său, joacă un rol de mediana si bisectoare, astfel încât tg (? / 2) = (b / 2) / h, din care h = b / (2tg (? / 2)) și redus la o formulă simplificată №5.

Deci, a cincea formula, ea spune asta. că zona poate fi găsit prin utilizarea înălțimii care își are originea în vârful triunghiului și se termină la baza sa, în același timp, împărțind-o în triunghiuri unghi drept. Și apoi, în a treia și a patra formule. Valoarea înălțimea podelei înmulțită cu baza.

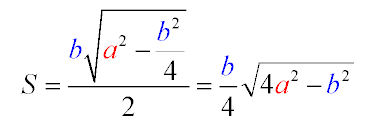
A șasea și ultima formulă. Ea apare în zona de soluții a unui triunghi de teorema lui Pitagora. Avem nevoie de înălțime, găsit în ultima formulă. Acesta reprezintă, de asemenea, pentru piciorul unui triunghi dreptunghic, obținem din lateral, plus jumătate din înălțimea de bază. partea ipotenuza este latura pătratului ipotenuzei (a) scade al doilea picior în pătrat. Deoarece el este egal cu podeaua - baza (b / 2), valoarea medie la pătrat = b2 / 4. Extragerea rădăcinii din rezultanta. găsi înălțimea.