prelegere №6

Interpolarea, polinoame de interpolare Lagrange și Newton.

problemă generală de interpolare. interpolare parabolic.

În rezolvarea multor probleme utilizând funcțiile de tabelă definite. De exemplu, dacă descoperim empiric o serie de valori ale unei funcții pentru a calcula valorile care nu sunt incluse în tabel, este posibil să se aleagă o altă, funcția mai simplu, într-un mod închide acest lucru.

Există diferite modalități de a obține aceste funcții. Unul dintre ei - interpolare.

În general, problema interpolării este formulată după cum urmează:

Fie n + 1 la punctele

Valorile date ale funcției

Necesar pentru a ridica un funktsiyuφ destul de simplu (x) care îndeplinesc următoarele condiții:

b) pentru valorile rămase ale x în domeniul ecuației aproximative trebuie să fie îndeplinite

Funcția φ (x) nazyvaetsyainterpoliruyuschey,

procesul construcției sale - prin interpolare,

și x0, x1, x2, ..., xn. în care valorile funcției interpolarea trebuie să coincidă cu valorile predeterminate ale funcției interpolarea -uzlami.

Un punct x. în care valoarea calculată a funcției f (x) prin funktsiiφ (x). interpolare nazyvaetsyatochkoy.

interpolare parabolic. Funcția interpolate este de obicei ales dintr-o anumită clasă de funcții. De multe ori, ca o astfel de funcție este luată mnogochlenFn (x), care nazyvaetsyainterpolyatsionnym polinomială.

Interpolarea folosind polinomului numit interpolare parabolic, sensul geometric al cărui este că graficul funcției f (x) este înlocuit cu un parabole-graph mnogochlenaFn (x); în timp ce grafica imeyutn + 1 punct comun.

Astfel, problema de interpolare parabolic este formulată după cum urmează:

Fie valorile funcției f (x) sunt setate la n + 1 nodul de interpolare

Ca un interpolate funcții polinomiale alege

și cer ca nodurile de valori de interpolare polinomului de interpolare coincid cu valorile acestei funcții:

Pentru a calcula coeficienții necunoscuți ai polinomului pe baza condiției (4) formează un sistem de ecuații:

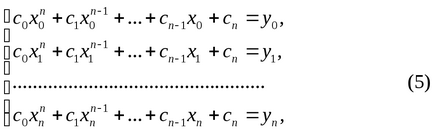
Formează determinantul sistemului (5):

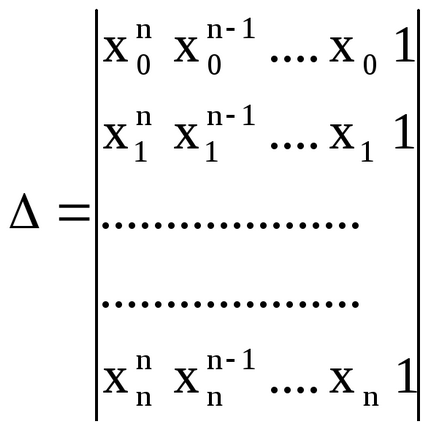
Acest factor determinant este cunoscut dintr-un curs de algebră mai mare ca un factor determinant Vandermonde.

Deoarece interpolare nodurile x0, x1, x2, ..., xn sunt diferite, atunci   0, prin urmare, sistemul liniar (5) are o soluție unică, ceea ce înseamnă existența și unicitatea polinomului de interpolare Fn (x).

Trebuie remarcat faptul că diferitele intrări ale polinomului de interpolare utilizate în rezolvarea diverselor probleme.

Lagrange de interpolare polinomială

Conform condițiilor (1), (2), prezentat la φ (x) funcția. mnogochlenn scrie gradul al doilea.

În același timp, ceilalți termeni ai polinomului (6) trebuie să fie zero, adică

Astfel, am formulat cerințele pentru pi factor (x). și anume:

pi Factor (x) polinomul nazyvayutvspomogatelnym stepenin.

Având în vedere proprietatea (8) și cerința ca pi polinomul (x) au stepenn. Noi scrie:

în care un coeficient ci.

Pentru a determina CI rândul său, la cerința (7). Din aceasta rezultă:

Făcând substituția (10) în (9) se obține expresia finală pentru pi (x):

polinom Construit (11), de exemplu, la punctul x0 primește znacheniep0 (x0) = 1, iar în alte noduri - valori egale cu zero.

P1 polinomiale (x) în tochkex1 va fi 1 iar nodurile rămase este egal cu 0, etc.

Astfel, pi polinomul auxiliar (x) satisface în totalitate cerințele (7), (8), iar al doilea mnogochlenn- gradul

Este Lagrange polinomului de interpolare.

Notă: Lagrange polinom adecvat să se utilizeze în sarcina restabilirii funcției f (x). atunci când punctul este mai aproape interpolyatsiix grila ktsentru.

Considerăm că funcția f (x). Specifică tabelul:

În consecință, construit satisface polinomiale condiția principală (1).

Astfel, testele algoritmul sunt următoarele:

set alternativ ca valorile xi puncte de masă și interpolarea pentru a obține valorile funktsiifi corespunzătoare (condiția trebuie să fie îndeplinite pentru programul de funcționare corespunzător (1)).

setați ca valorile de interpolare de mai mulți pixeli care nu sunt noduri ale rețelei și verificați starea (2).

Estimarea erorii formula Lagrange de interpolare

Diferența Rn (x) Membrul nazyvaetsyaostatochnym formula lui Lagrange. ZnachenieRn (x) este egal cu eroarea, care se obține prin înlocuirea valorilor funcției f (x) interpolare valoarea mnogochlenaFn (x).

este posibil să se obțină o formulă pentru termenul rest

Formula (13) poate fi scrisă în mod diferit:

atunci obținem o estimare a restului:

Exemplu. Pentru funktsiiu = 2x construi interpolare polinomul Lagrange prin interpolarea noduri point

Se calculează valorile corespunzătoare ale funcției:

Formula lui Lagrange găsim:

Estimăm eroarea care se obține prin înlocuirea funcției y = 2x mnogochlenomF3 (x). derivat al patrulea ordin

In intervalul [-1; 2] crește funktsiya2x, astfel 0<2x <= 4.

Prin formula (15) obținem:

Lagrange polinom este Considerat folosit în general în problemele de restabilire a funcției f (x). atunci când punctul de interpolare este situat mai aproape de centrul grilei.

Dacă punctul de interpolare x este situată mai aproape de marginile grilei, este mai bine să utilizați polinom lui Newton. Există două posibilități:

punct de interpolare x este vblizipervogo nod setkih0 (NyutonaI polinomial);

punct de interpolare x este nodul setkihn vbliziposlednego (NyutonaII polinomial).

Notă. Construcții Lagrange polinomul bazat pe mnogochlenepi Sub (x).

Baza construcției este conceptul de polinomiale a diferenței finite a lui Newton.

Noi definim noțiunea de diferență finită.

Lăsați masa funcție este setată cu o shagomh constantă: